In this week’s free episode of Deke’s Techniques, Deke begins a deep dive into tessellating irregular convex pentagons. Because, you know, if there’s anything Deke can get totally obsessed with, it’s math meets art, with a side of pattern-making. It’s a recipe for a dekeDive.

He begins with a discussion of a simple, regular pentagon in which all the angles and side lengths are the same.

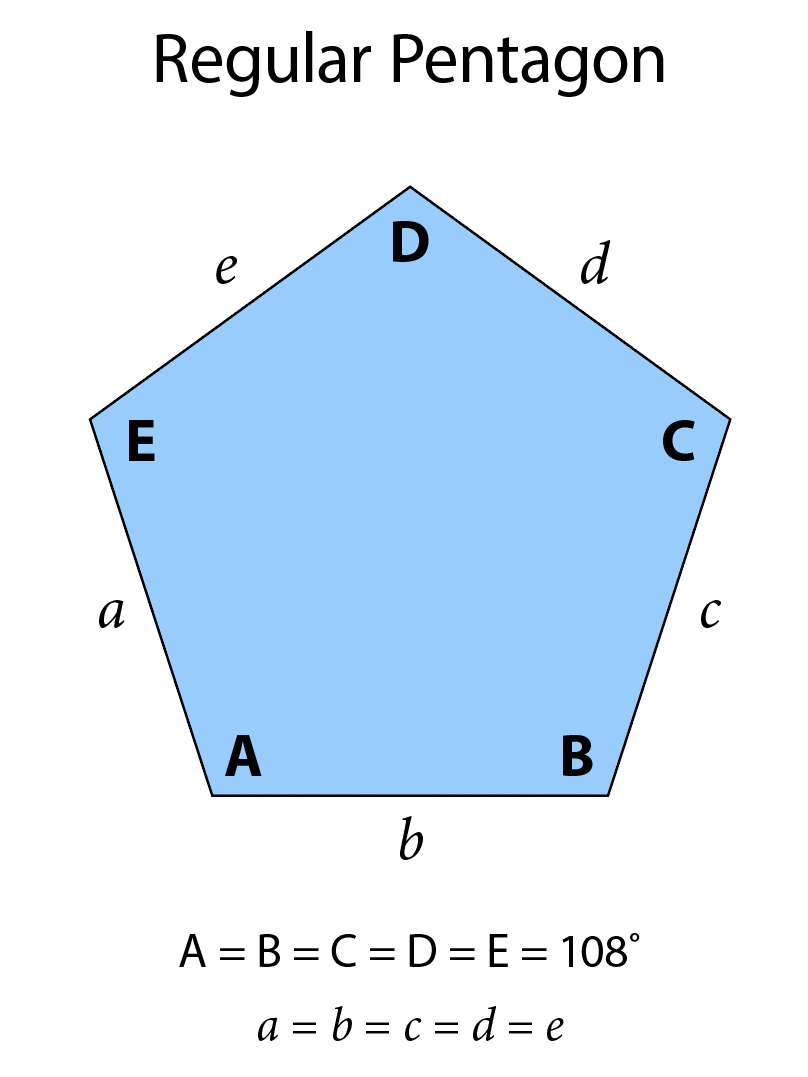
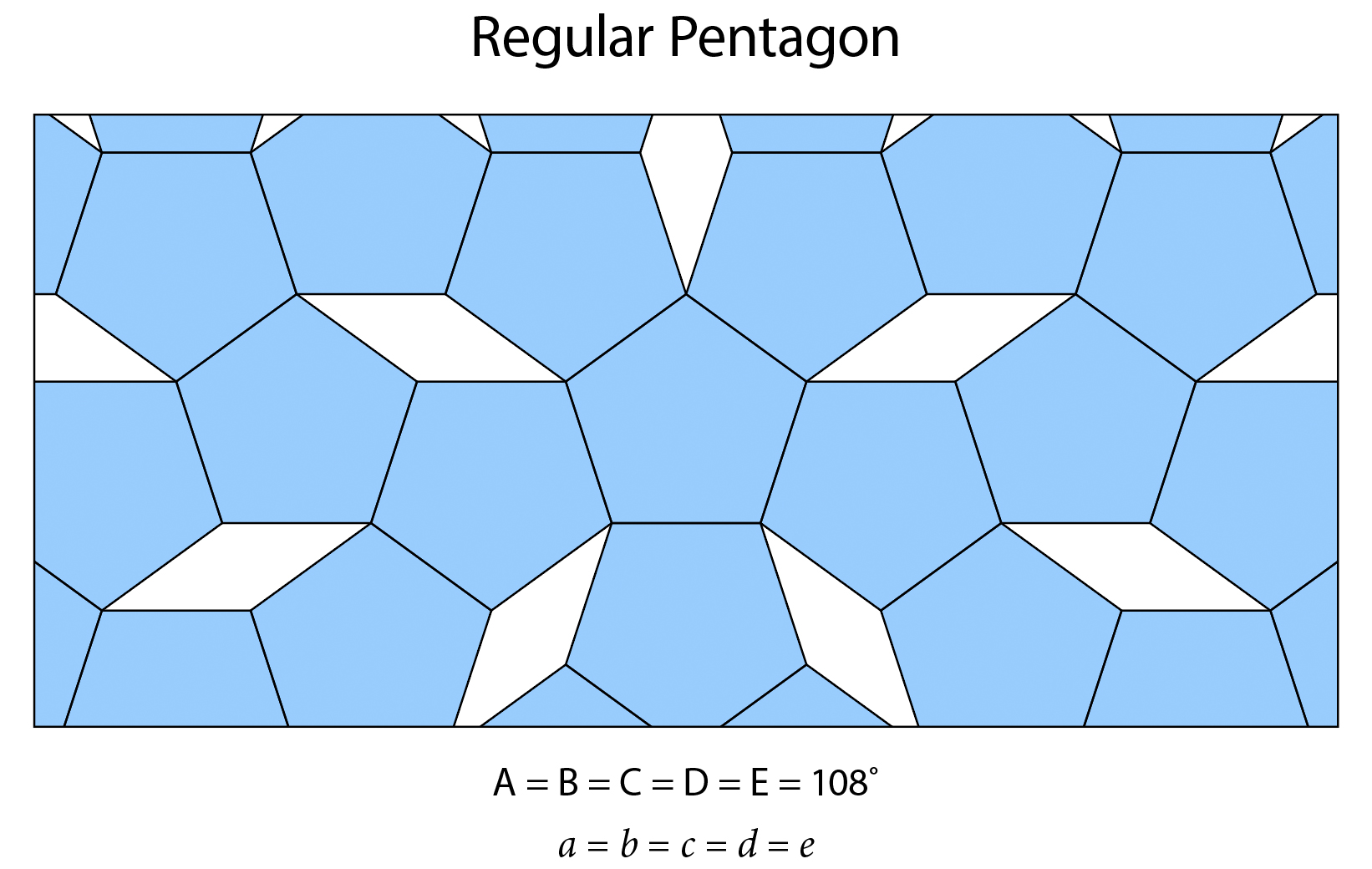
Which, makes for a cool pattern, but it does not tessellate on its own. (Not without the addition of some filler diamond shapes.)

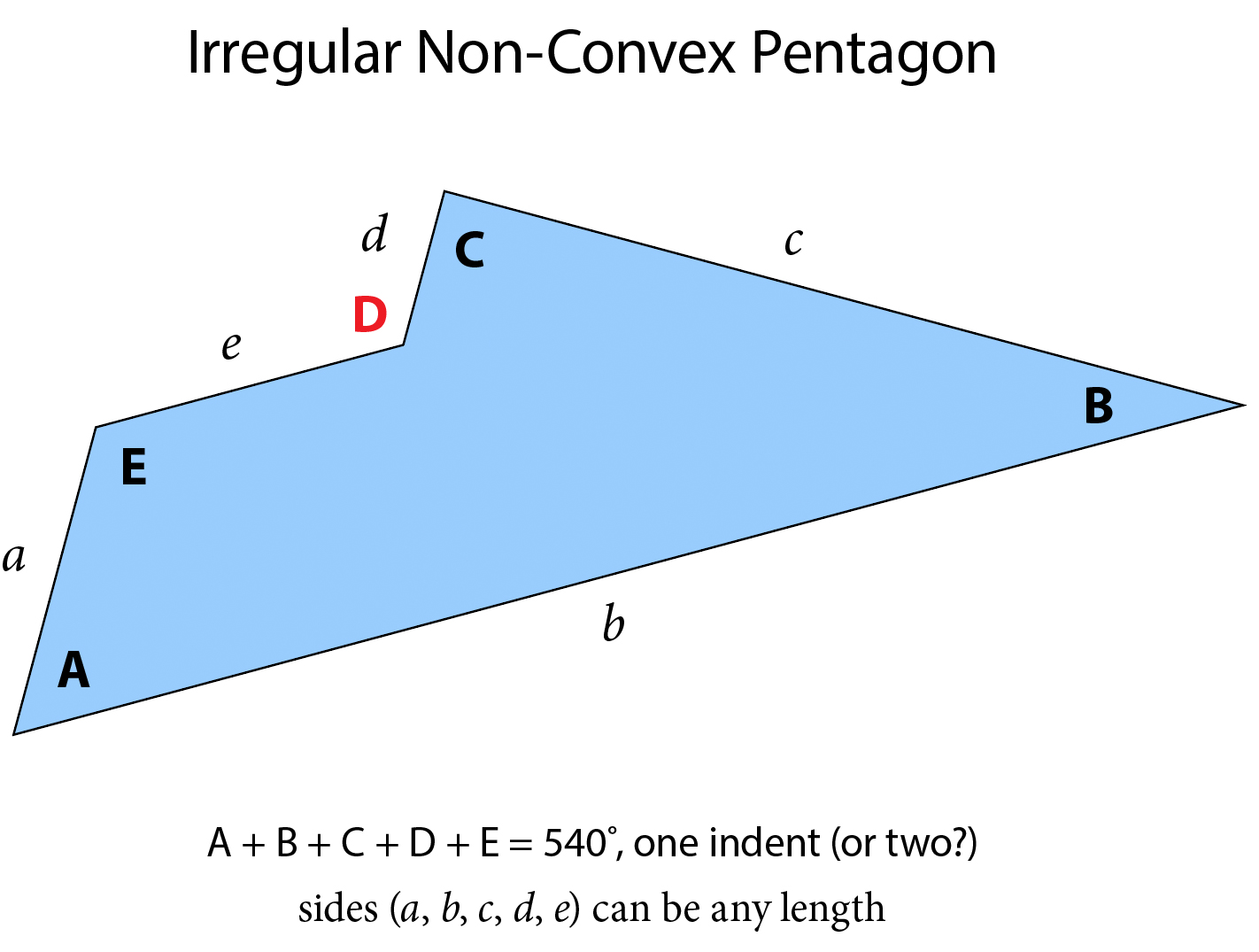
Meanwhile, an irregular non-convex pentagon (i.e., in which one of the angles indents), like this:

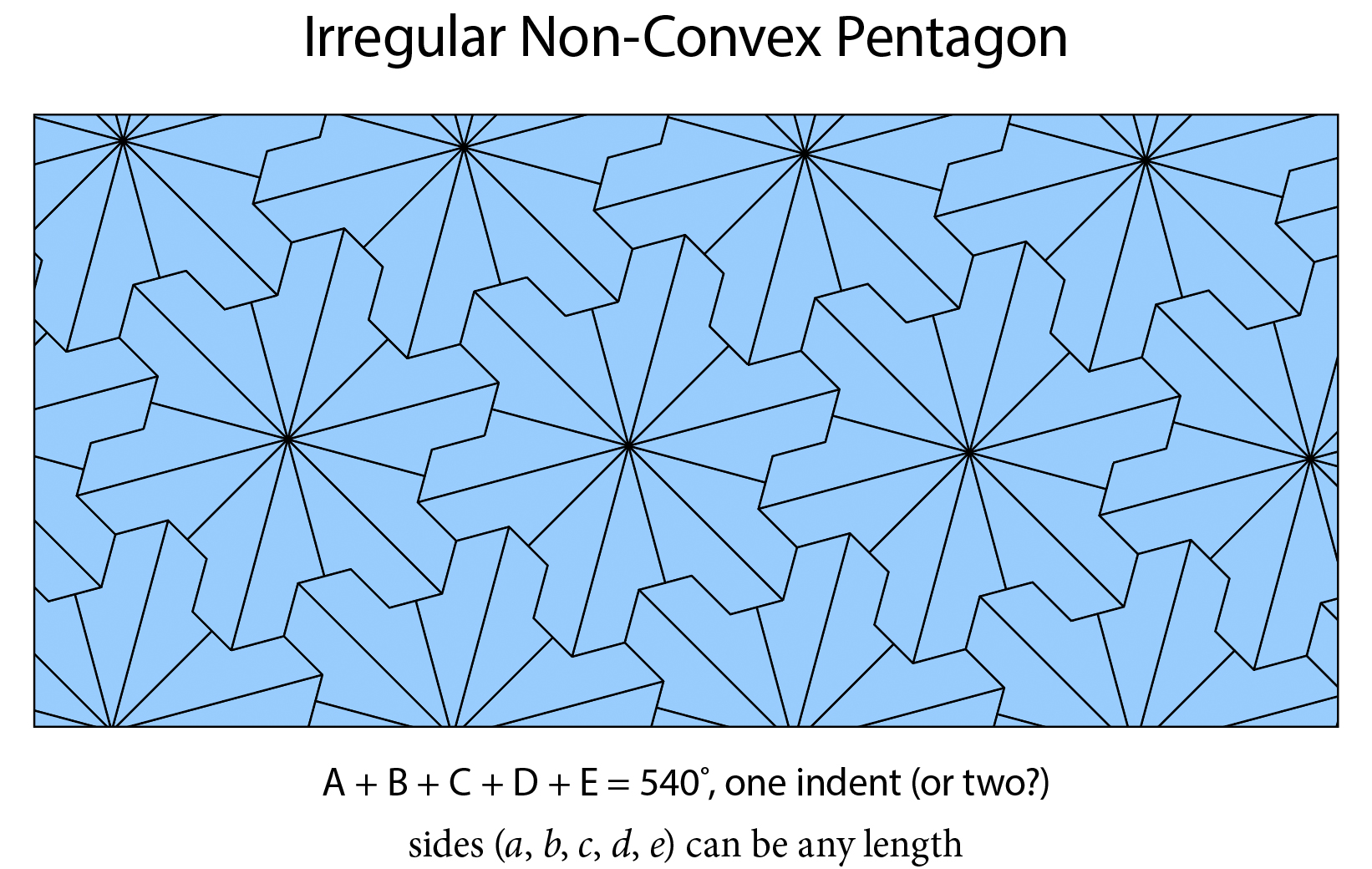
...creates an interesting pattern, about which Deke manages to avoid going down a tangential rabbit hole. But here it is anyway.

And finally, we have one—of fifteen, apparently, so far, maybe forever—irregular convex pentagonal shapes, like this one for instance:

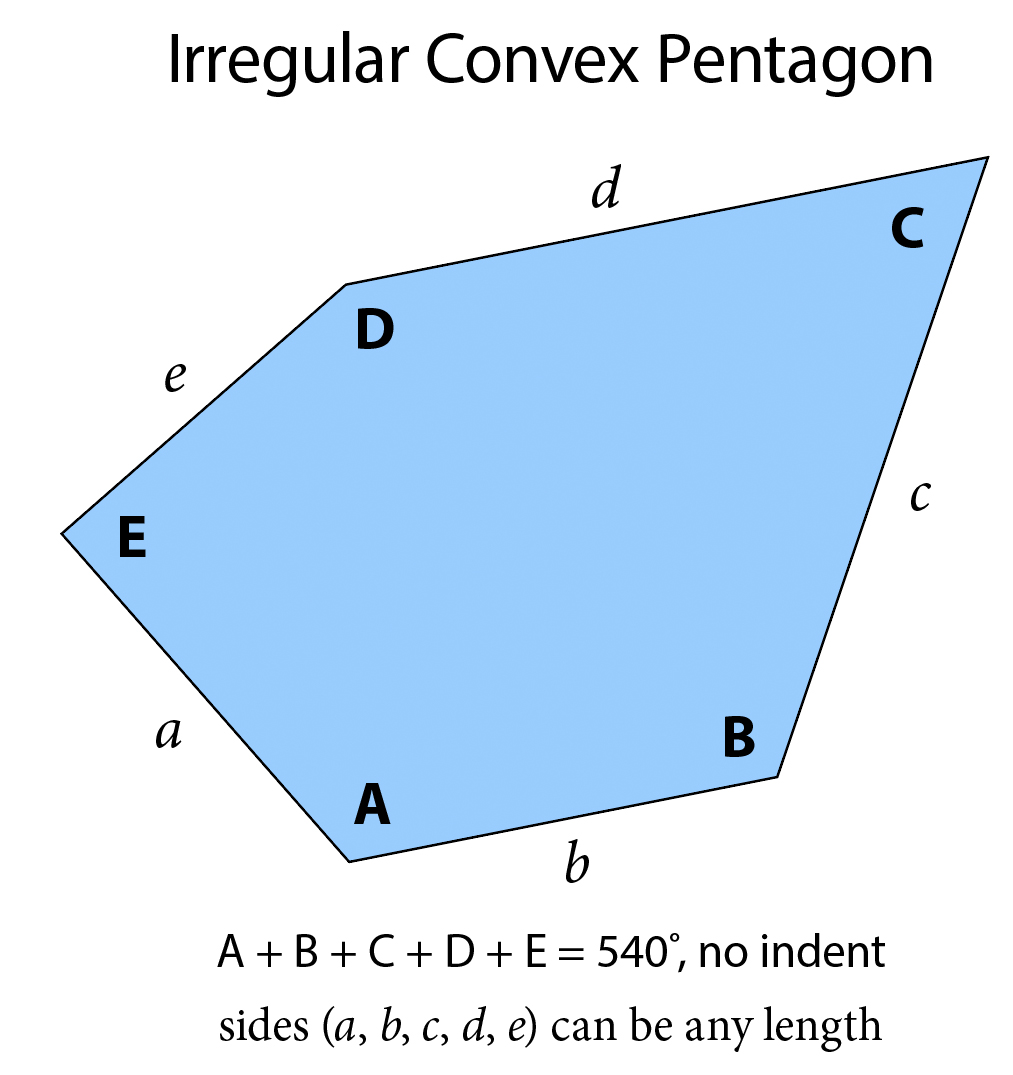
Which yields this intriguing and beautiful tessellation:

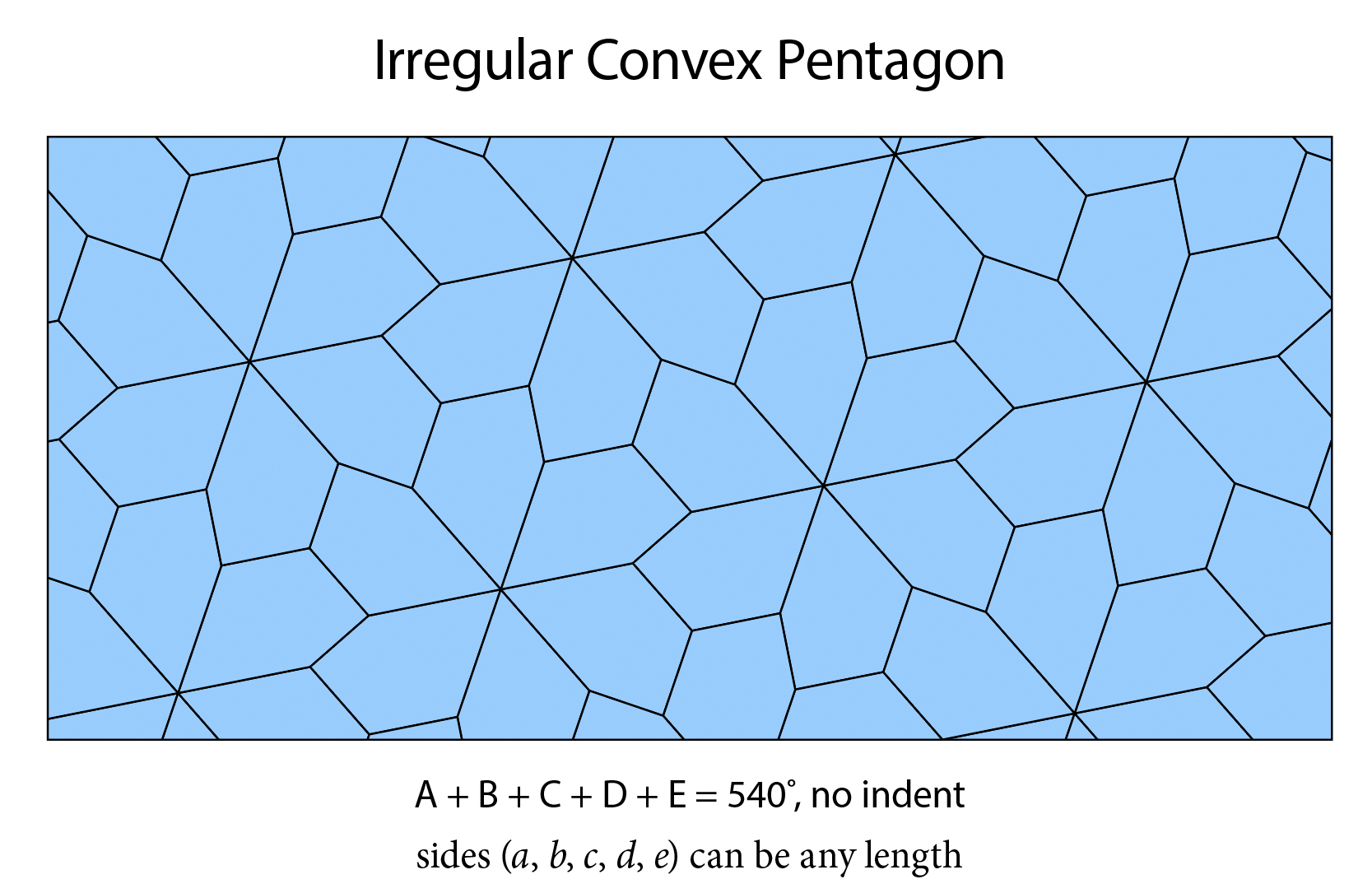
In the next few weeks, you’re bound to find out all about which irregular pentagons actually yield which results. (Like the one at the top of this post, Number 12, discovered in 1977 by Marjorie Rice, a mom and amateur mathematician who would smoke the rest of us in the art of pattern-making.)

Oh, and speaking of recipes (were we?), in case you missed it over on Deke’s Instagram thing: Here is how I put Deke’s special gradient-making talents to work for a cocktail party we were hosting. I give you the Deconstructed Gradient Caprese Salad. Deke’s pretty handy to have around sometimes.

Deke’s Techniques, where math and art and geekery and tomatoes converge!